Deep Spline Neural Networks
@BIG.EPFL

Note: It might be useful to read this project's introduction too.

Suppose we have a dataset \({\mathrm D}\) that consists of sequence of \(M\) images of cats and dogs, together with their respective labels. Mathematically, we write this statement as \({\mathrm D} = \lbrace{\mathbf x}_m, y_m\rbrace _{m=1}^M\), where \(y_m = 0\) if \({\mathbf x}_m\) represents a cat, and \(y_m = 1\) otherwise, as depicted below.

In supervised learning, our goal is to find a model \(f\) that makes few classification mistakes for the images in our dataset 1 as well as new images that are not found in the training data 2 3.

Mathematical Details

In the cat-or-dog example, the output of our model is a two-element vector where each value represents the "confidence" in each label, and the predictions \({\hat y}_m\) are assigned according to the label with the highest confidence; that is, $$ \begin{align*} f({\mathbf x}_m) & = (a_{m,0}, a_{m,1}) \\[5pt] {\hat y}_m & = \begin{cases} 0 & \text{if} \ \ a_{m,0} \geq a_{m,1} \\ 1 & \text{if} \ \ a_{m,0} < a_{m,1} \end{cases} \end{align*} $$

Neural Networks

Nowadays, neural networks are the most standard way of solving supervised learning problems. Neural nets are sequences of simple linear transformations and pointwise nonlinearities called activation functions 4. The most popular activation function is the ReLU, which is a continuous and piecewise-linear (CPWL) function, meaning that its graph is composed of straight-line segments (like this 📉). Interestingly, networks with CPWL activations are CPWL functions themselves.

A Bit of Theory

In order to learn the activation functions of a neural network, we need a way to turn them into learnable modules that depend on discrete parameters, as is the case with the linear transformation 5. To do this, we have to introduce some constraints.

Since networks with CPWL activations seem to work very well, it would be great if we could mantain this behaviour. Well, it turns out that we can modify our problem statement slightly by adding a regularization term called "second-order total variation", and have guarantees that there are optimal solutions to the problem (i.e., optimal models) that actually have CPWL activation functions. In that case, we have a theoretical justification to restrict our search to such kinds of models. (For example, if you are looking for a very fast bike in a big bike shop, and someone tells you that the last Tour de France was won with a bike of this particular brand, then it's smarter to just try out bikes from that specific brand because you know that at least one of them will do the job well.)

The First Project: Deep Spline Networks

(There are a few important steps in getting from the theory to the actual algorithm that we have ommited here for the sake of simplicity. If you'd like to know more details, you can read the corresponding article.)

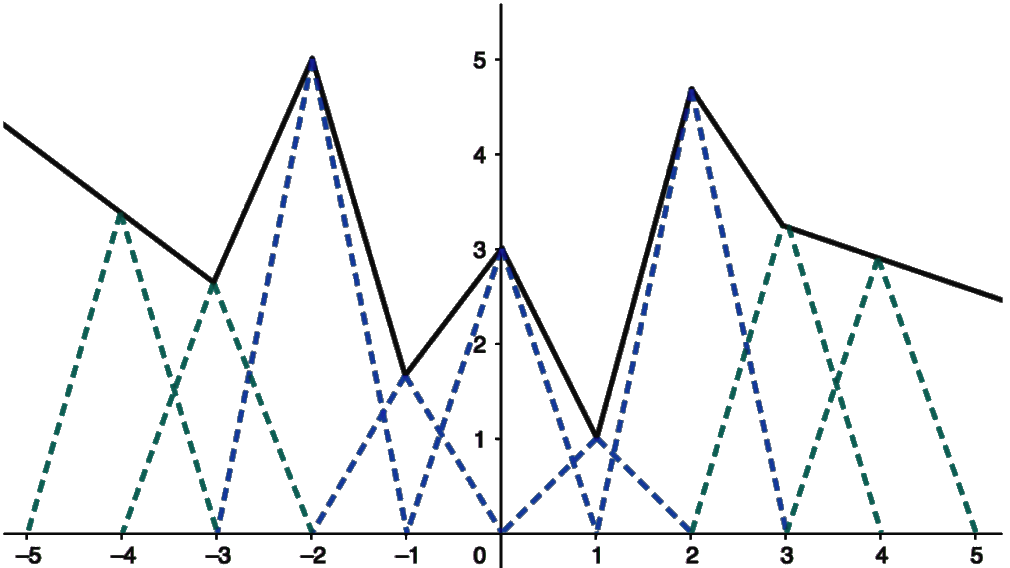
In order to have learnable activation functions, we construct them using "lego pieces" (basis functions) called \(\beta ^1\)-splines, which are placed at equally-spaced locations. In the image at the top, you can see how several lego pieces work together to form a parametrized activation function 6. During training, we learn the heights (coefficients) of the lego pieces together with the other parameters in the network. The models that can be found using our method are called "deep spline networks"; they include all models with ReLU-like activations (ReLU, LeakyReLU, PReLU, etc.).

Apart from being theoretically supported, our method has two practical key strengths: First, the output of the activatons at a specific location depends on (at most) two lego pieces because the lego pieces are localized, meaning that they are zero outside a small range. 7. This makes our method is stable (well-conditioned), and fast to run. Second, we can control the degree of simplicity of our activations—as measured by the number of knots/linear regions—by changing the strength of the regularization applied 8. Therefore, our approach compatible with the Occam's razor principle: as long as it can do the job, the simpler, the better. Simple models have the advantage of being lighter (ocupying less memory) and faster. Moreover, they are more explainable/interpretable: if they make a prediction error, we have a better chance of actually understanding what went wrong (*cough* ChatGPT *cough*) 9.

In terms of results, we have observed that our method compares favorably to the traditional ReLU networks, with the improvement being more pronounced for simpler/smaller networks.

The Second Project: Deep Spline Networks with Controlled Lipschitz Constant

In this work, we modified "slightly" the regularization term used in the previous work—the new version being called "second-order bounded variation"—and showed that this allowed us to control the Lipschitz constant of the network, which measures how robust the network's predictions are to small changes in the input. This is very important to ensure the reliability of neural nets. For example, we dont't want self-driving cars to not be able to detect stop signs if someone graffitied them or pasted small stickers on top. Unfortunately, this has been shown to happen with standard neural nets in this paper: a clear example of how a lack of robustness can lead to tragic consequences.

Publications

Impact

The foundational work on deep spline neural networks has been cited over 34 times in the scientific literature; the second work on the lipschitz control of such networks has been cited over 36 times.

Code & Tech Stack

This work resulted in the publication of a Pypi package called deepsplines. The code for this project can be found in this Github Repository. Here, I outline a few technologies that were used:

• Python: Programming language.
• Pytorch: Deep learning framework.
• Bash: Unix shell and command language.

Acknowledgments

I would like to thank my supervisor, Shayan Aziznejad, and Professor Michael Unser for their kindness and insight.